Simulations exogenous shocks

In this document, I run a simulation exercise to illustrate how using a exogenous shocks to avoid confounders may lead to a loss in power and inflated effect sizes. To make these simulations realistic, I emulate a typical study estimating the impact of air pollution reduction shocks on birthweight of newborn babies.

Show packages 
library(tidyverse) 
library(knitr) 
library(fixest)
library(mediocrethemes)
library(broom)
library(tictoc)
library(here)
library(beepr)
library(ggdag)
library(modelsummary)

set_mediocre_all(pal = "coty")
set.seed(12)

Summary and intuition

A trade-off mediated by the number of treated observations

In the case of studies using exogenous shocks, a confounding-exaggeration trade-off is mediated by the number of (un)treated observations. In some settings, while the number of observations is large, the number of events might be limited. Pinpointing exogenous shocks is never easy and we are sometimes only able to find a limited number of occurrences of this shock or shocks affecting a small portion of the population. More precisely, the number of observations with a non-null treatment status might be small (or conversely the number of non-treated units might be small). In this instance, the variation available to identify the treatment is limited, possibly leading power to be low and exaggeration issues to arise.

An illustrative example

For readability and to illustrate this loss in power, let’s consider an example setting. For this illustration we could use a large variety of Data Genereting Processes (DGP), both in terms of distribution of the variables and of relations between them. I narrow this down to an example setting, considering an analysis of health impacts of air pollution. More precisely, I simulate and analyze the impacts of air pollution reduction in birthweights. Air pollution might vary with other variables that may also affect birthweight (for instance economic activity). Some of these variables might be unobserved and bias estimates of a simple regression of birthweight on pollution levels. A strategy to avoid such issues is to consider exogenous shocks to air pollution such as plant closures, plant openings, creation of a low emission zone or an urban toll, strikes, etc.

Although I consider an example setting for clarity, this confounding-exaggeration trade-off mediated by a number of treated observations arises in other settings.

Modeling choices

To simplify, I make the assumptions described below. Of course these assumptions may be seen as arbitrary and I invite interested readers to play around with them.

Many studies in the literature, such as Currie et al. (2015) and Lavaine and Neidell (2017) for instance, aggregate observations to build a panel. I follow this approach and look at the evolution of birthweights in zip codes in time.

Here, I only estimate a reduced form model and am therefore not interested in modeling the effect of the plant closure on pollution levels. I consider that the plant closure leads to some air pollution reduction and want to estimate the effect of this closure on birth-weight.

The DGP can be represented using the following Directed Acyclic Graph (DAG):

Show code 
second_color <- str_sub(colors_mediocre[["four_colors"]], 10, 16)

dagify(W ~ T + zFE + tFE + u,
       exposure = c("W", "T", "zFE", "tFE"),
       # outcome = "w",
       latent = c("u"),
       coords = list(x = c(W = 3, T = 2, zFE = 2.5, tFE = 2.5, u = 3),
                     y = c(W = 1, T = 1, zFE = 0, tFE = 2, u = 2))
  ) |> 
  ggdag_status(text_size = 5) +
  theme_dag_blank(legend.position = "none") +
  scale_mediocre_d(pal = "coty") + 
  annotate(#parameters
    "text", 
    x = c(2.5), 
    y = c(1.1), 
    label = c("beta"),
    parse = TRUE,
    color = "black",
    size = 5
  )

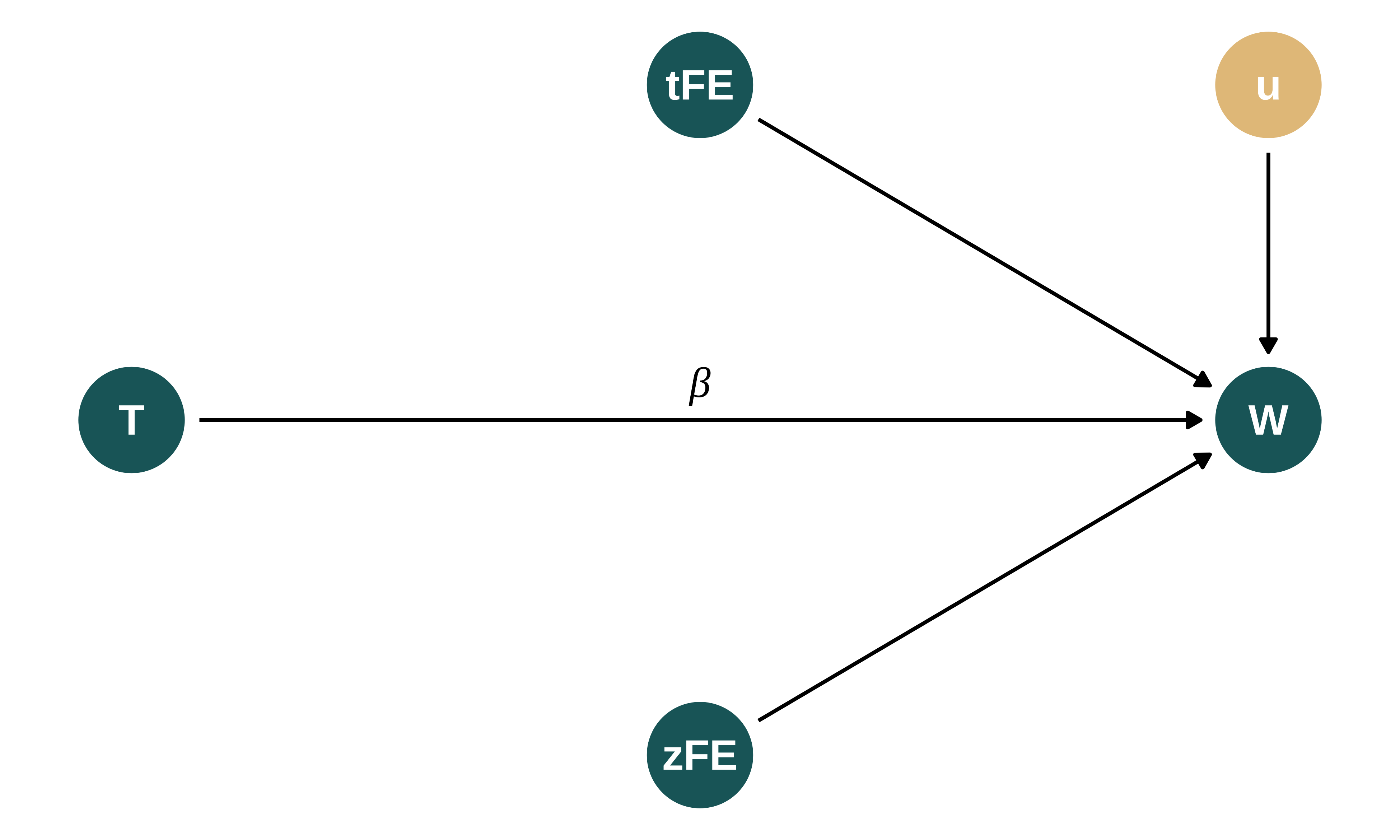
I consider that the average birthweight in zip code \(z\) at time period \(t\), \(w_{zt}\), depends on a zip code fixed-effect \(\zeta_z\), a time fixed-effect \(\tau_t\) and the treatment status \(T_i\), ie whether a plant is closed in this period or not. For now, I do not simulate omitted variable biases as I consider that the shocks are truly exogenous. Thus, birthweight is defined as follows:

\[w_{zt} = \beta_0 + \beta_1 T_{zt} + \zeta_z + \tau_t + u_{zt}\]

To simplify, I consider the following additional assumptions:

More precisely, I set:

Data generation

Generating function

I write a simple function that generates the data. It takes as input the values of the different parameters and returns a data frame containing all the variables for this analysis.

generate_data_shocks <- function(N_z,
                                 N_t,
                                 p_treat,
                                 sigma_u,
                                 beta_0,
                                 beta_1,
                                 mu_zip_fe, 
                                 sigma_zip_fe,
                                 mu_time_fe, 
                                 sigma_time_fe) {
  
  tibble(zip = 1:N_z) |> 
    crossing(t = 1:N_t) |>
    group_by(zip) |>
    mutate(zip_fe = rnorm(1, mu_zip_fe, sigma_zip_fe)) |>
    ungroup() |>
    group_by(t) |>
    mutate(time_fe = rnorm(1, mu_time_fe, sigma_time_fe)) |>
    ungroup() %>%
    mutate(
      id = row_number(),
      treated = (id %in% sample(1:(N_z*N_t), floor(N_z*N_t*p_treat))),
      u = rnorm(nrow(.), 0, sigma_u),
      birthweight0 = beta_0 + zip_fe + time_fe + u,
      birthweight1 = birthweight0 + beta_1,
      birthweight = treated*birthweight1 + (1 - treated)*birthweight0
    )
}

Calibration and baseline parameters’ values

I set baseline values for the parameters to emulate a somehow realistic observational study`. I get “inspiration” for the values of parameters from Lavaine and Neidell (2017), Currie et al. (2015) and an additional study that uses a different identification strategy to study the same question: Yang and Chou (2018). The former investigates the impact of oil refinery strikes in France on birth-weight and gestational age of newborn. The latter studies the impact of air pollution from plants (openings and closures) on WTP (housing value) and health (incidence of low birthweights).

I consider that:

N_z N_t p_treat sigma_u beta_0 beta_1 mu_zip_fe sigma_zip_fe mu_time_fe sigma_time_fe
2000 50 0.1 430 3163 30 33 90 33 90

Here is an example of variables created with the data generating process and baseline parameter values, for 2 zip codes and 8 time periods (not displaying parameters):

Show code 
baseline_param_shocks |>  
  mutate(N_z = 2, N_t = 8, p_treat = 0.5) |> 
  pmap(generate_data_shocks) |>  #use pmap to pass the set of parameters
  list_rbind() |> 
  select(zip, t, treated, starts_with("birthweight"), u, ends_with("fe")) |>  
  kable()
zip t treated birthweight0 birthweight1 birthweight u zip_fe time_fe
1 1 FALSE 3156.062 3186.062 3156.062 146.42028 -100.2511 -53.107003
1 2 FALSE 3230.945 3260.945 3230.945 217.99631 -100.2511 -49.800472
1 3 FALSE 2789.840 2819.840 2789.840 -126.12121 -100.2511 -146.787789
1 4 TRUE 3167.408 3197.408 3197.408 96.16581 -100.2511 8.493356
1 5 FALSE 3930.464 3960.464 3930.464 863.09663 -100.2511 4.618616
1 6 FALSE 3474.357 3504.357 3474.357 435.15102 -100.2511 -23.542971
1 7 TRUE 2956.110 2986.110 2986.110 -130.05748 -100.2511 23.418250
1 8 TRUE 2693.415 2723.415 2723.415 -440.85528 -100.2511 71.521332
2 1 TRUE 3169.863 3199.863 3199.863 -114.97548 174.9453 -53.107003
2 2 FALSE 3202.529 3232.529 3202.529 -85.61543 174.9453 -49.800472
2 3 FALSE 3247.540 3277.540 3247.540 56.38272 174.9453 -146.787789
2 4 TRUE 3409.133 3439.133 3439.133 62.69396 174.9453 8.493356
2 5 TRUE 3498.252 3528.252 3528.252 155.68783 174.9453 4.618616
2 6 TRUE 3604.214 3634.214 3634.214 289.81190 174.9453 -23.542971
2 7 FALSE 4252.339 4282.339 4252.339 890.97538 174.9453 23.418250
2 8 TRUE 3176.824 3206.824 3206.824 -232.64232 174.9453 71.521332

A quick check on a full data set shows that the standard deviation and mean of the birthweight correspond to what we aimed for:

Show code 
ex_data_shocks <- baseline_param_shocks |> 
  pmap(generate_data_shocks) |> 
  list_rbind()

ex_data_shocks_mean <- ex_data_shocks |> 
  summarise(across(.cols = c(birthweight0), mean)) |> 
  mutate(Statistic = "Mean") |> 
  select(Statistic, everything())

ex_data_shocks_sd <- ex_data_shocks |> 
  summarise(across(.cols = c(birthweight0), stats::sd)) |> 
  mutate(Statistic = "Standard Deviation") |> 
  select(Statistic, everything())

ex_data_shocks_mean |> 
  rbind(ex_data_shocks_sd) |> 
  kable()
Statistic birthweight0
Mean 3234.4969
Standard Deviation 447.6321

The treatment allocation when the proportion of treated zip codes is 10% is as follows:

Show code 
baseline_param_shocks |> 
  mutate(N_z = 20, N_t = 50) |>
  pmap_dfr(generate_data_shocks) |> 
  mutate(treated = ifelse(treated, "Treated", "Not treated")) |> 
  ggplot(aes(x = t, y = factor(zip), fill = fct_rev(treated))) + 
  geom_tile(color = "white", lwd = 0.3, linetype = 1) +
  coord_fixed() +
  scale_y_discrete(breaks = c(1, 5, 10, 15, 20)) +
  labs(
    title = "Treatment assignment across time and zip codes",
    x = "Time index", 
    y = "Zip code id", 
    fill = NULL
  )

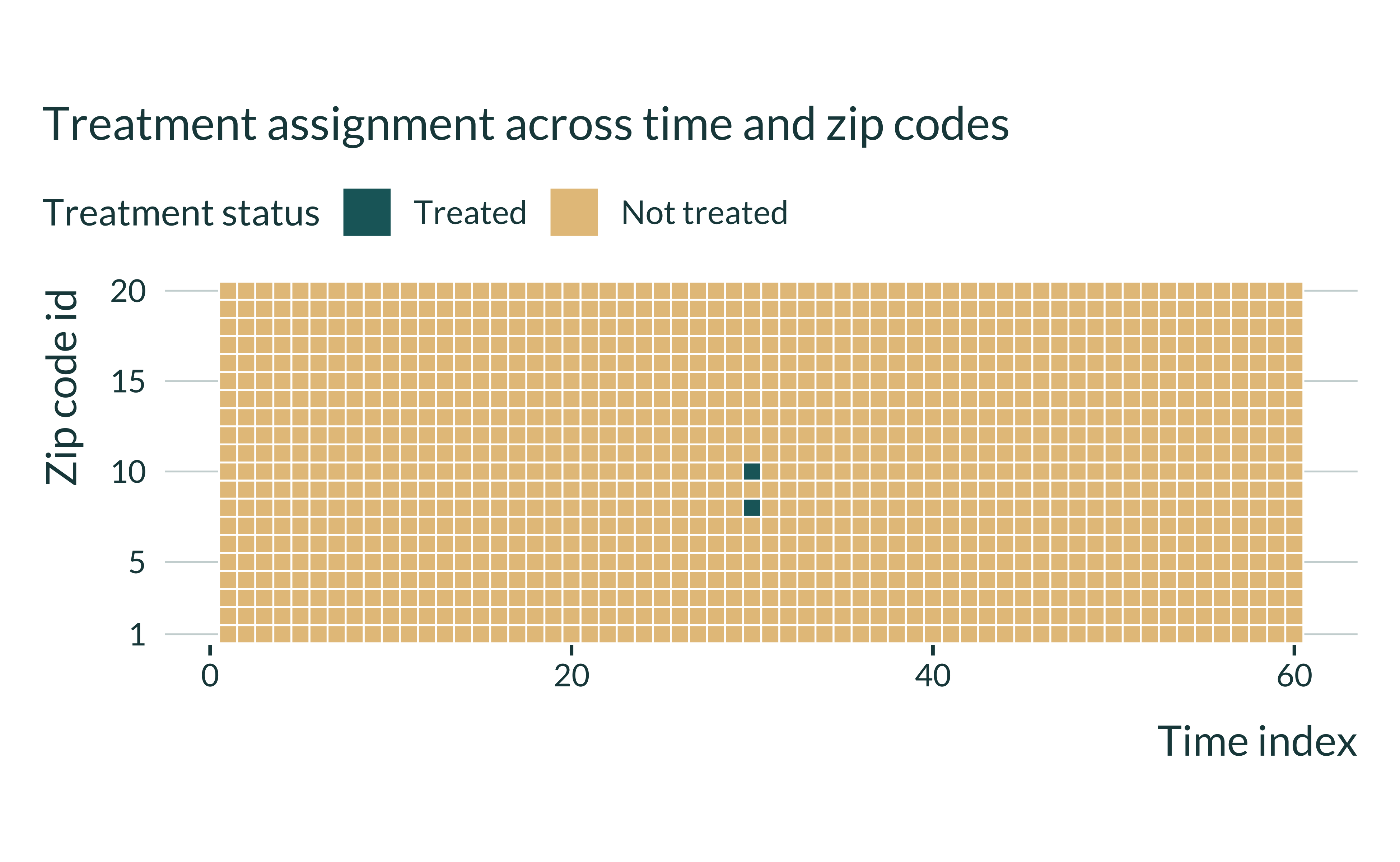
Under this set of parameters, a very limited number of observations are treated.

Quick data exploration

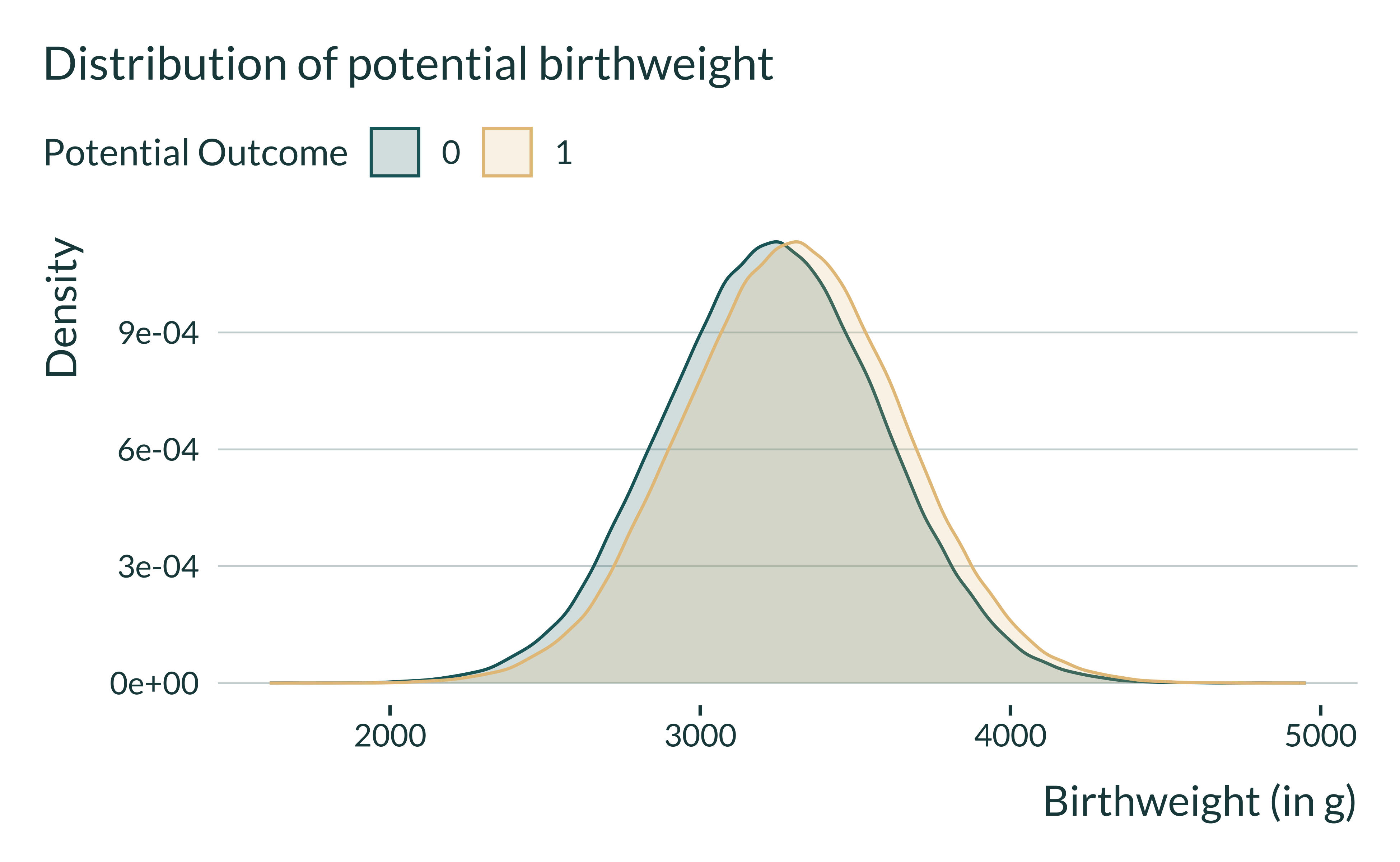
I quickly explore a generated data set to get a sense of how the data is distributed. First, I display the distribution of potential outcomes.

Show code 
ex_data_shocks |> 
  pivot_longer(
    cols = c(birthweight0, birthweight1),
    names_to = "potential_outcome",
    values_to = "potential_birthweight"
  ) |> 
  mutate(potential_outcome = factor(str_remove(potential_outcome, "birthweight"))) |> 
  ggplot(aes(x = potential_birthweight, fill = potential_outcome, color = potential_outcome)) +
  geom_density() +
  labs(
    x = "Birthweight (in g)",
    y = "Density",
    color = "Potential Outcome",
    fill = "Potential Outcome",
    title = "Distribution of potential birthweight"
  )

Estimation

I then define a function to run the estimation.

I cluster the standard error by zip code and time period. Lavaine and Neidell (2017) cluster standard error at the month and department level and Currie et al. (2015) at the plant-year level. They therefore both cluster at the period and group of units level, a higher level than mine.

estimate_shocks <- function(data) {
  reg <- 
    feols(data = data, fml = birthweight ~ treated | zip + t, vcov = "twoway") |> 
    broom::tidy() |>
    rename(p_value = p.value, se = std.error) |>
    select(-statistic) 
  
  return(reg)
}

Here is an example of an output of this function:

term estimate se p_value
treatedTRUE 35.44544 4.82837 0

To double check the \(R^2\), I also display the output of a regression:

Show code 
reg_ex <- baseline_param_shocks |> 
  pmap_dfr(generate_data_shocks) |> 
  feols(fml = birthweight ~ treated | zip + t, vcov = "twoway") 

modelsummary::modelsummary(
  list("Birthweight" = reg_ex),
  gof_omit = "IC|Within|F|RMSE|Log"
)
Birthweight
treatedTRUE 27.634
(3.834)
Num.Obs. 100000
R2 0.098
R2 Adj. 0.079
Std.Errors by: zip & t

One simulation

I now run a simulation, combining generate_data_shocks and estimate_shocks. To do so I create the function compute_sim_shocks. This simple function takes as input the various parameters. It returns a table with the estimate of the treatment, its p-value and standard error, the true effect and the proportion of treated units. Note that for now, I do not store the values of the other parameters for simplicity because I consider them fixed over the study.

Show code 
compute_sim_shocks <- function(...) {
  args <- list(...)
  
  data <- generate_data_shocks(...)
  
  data <- data |>
    estimate_shocks() |> 
    mutate(
      N_z = args$N_z,
      N_t = args$N_t,
      p_treat = args$p_treat,
      true_effect = args$beta_1,
      n_treated = sum(data$treated)
    )
  
  gc()
  
  return(data)
}

Here is an example of an output of this function.

term estimate se p_value N_z N_t p_treat true_effect n_treated
treatedTRUE 33.65475 4.155194 0 2000 50 0.1 30 10000

All simulations

I will run the simulations for different sets of parameters by looping the compute_sim_shocks function over the set of parameters. I thus create a table with all the values of the parameters to test, param_shocks. Note that in this table each set of parameters appears N_iter times as we want to run the analysis \(n_{iter}\) times for each set of parameters.

vect_p_treat <- c(0.0005, 0.001, 0.0024, 0.005, 0.01, 0.02)
n_iter <- 1000

param_shocks <- baseline_param_shocks |> 
  select(-p_treat) |> 
  crossing(vect_p_treat) |> 
  rename(p_treat = vect_p_treat) |> 
  crossing(rep_id = 1:n_iter) |> 
  select(-rep_id)

I then run the simulations by looping our compute_sim_shocks function on param_shocks using the purrr package (pmap_dfr function).

tic()
sim_shocks <- pmap(param_shocks, compute_sim_shocks, .progress = TRUE) |> 
  list_rbind()
beep()
toc()

saveRDS(sim_shocks, here("Outputs/sim_shocks.RDS"))

Analysis of the results

Quick exploration

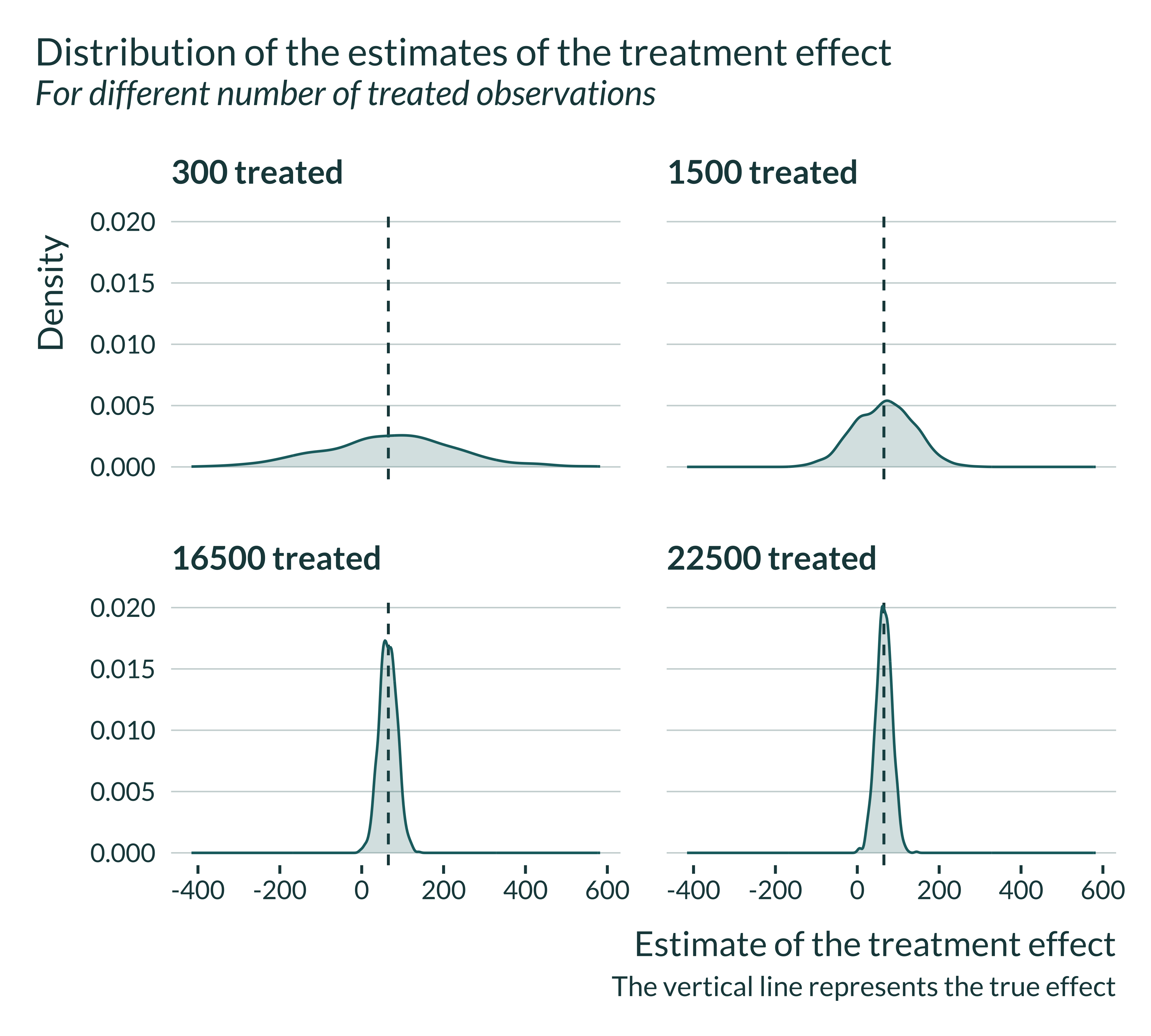
First, I quickly explore the results. I plot the distribution of the estimated effect sizes, along with the true effect. The estimator is unbiased and recover, on average, the true effect:

Show code 
sim_shocks <- readRDS(here("Outputs/sim_shocks.RDS"))

sim_shocks |> 
  filter(p_treat %in% sample(vect_p_treat, 4)) |>  
  mutate(
    n_treat_name = fct_inseq(paste(n_treated)),
    N_z = paste("Number zip codes: ", str_pad(N_z, 2)),
    N_t = paste("Number periods: ", str_pad(N_t, 2))
  ) |> 
  ggplot(aes(x = estimate)) +
  geom_vline(xintercept = unique(sim_shocks$true_effect)) +
  geom_density() +
  facet_wrap(~ fct_relabel(n_treat_name, \(x) paste(x, "treated")), nrow = 2) +
  labs(
    title = "Distribution of the estimates of the treatment effect",
    subtitle = "For different number of treated observations",
    x = "Estimate of the treatment effect",
    y = "Density",
    caption = "The vertical line represents the true effect"
  )

Computing bias and exaaggeration ratio

We want to compare \(\mathbb{E}\left[ \left| \frac{\widehat{\beta_{red}}}{\beta_1}\right|\right]\) and \(\mathbb{E}\left[ \left| \frac{\widehat{\beta_{red}}}{\beta_1} \right| | \text{signif} \right]\). The first term represents the bias and the second term represents the exaggeration ratio. These terms depend on the true effect size.

source(here("functions.R"))

summary_sim_shocks <- 
  summarise_sim(
    data = sim_shocks |> mutate(true_effect = round(true_effect)), 
    varying_params = c(p_treat, n_treated, N_t, N_z), 
    true_effect = true_effect
  ) 

# saveRDS(summary_sim_shocks, here("Outputs/summary_sim_shocks.RDS"))

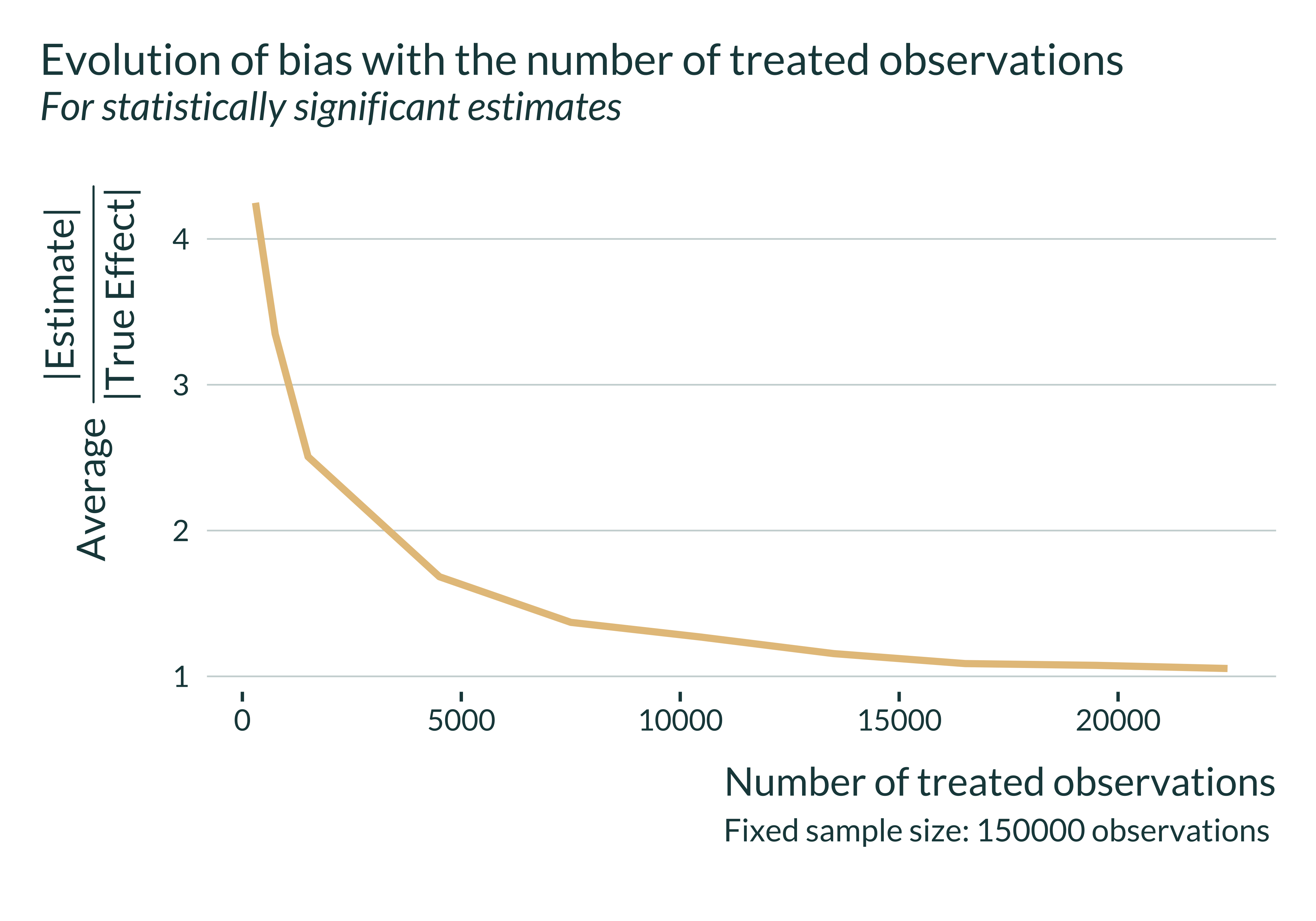
Main graph

To analyze our results, I build a unique and simple graph:

Show code 
summary_sim_shocks |> 
  ggplot(aes(x = n_treated, y = type_m)) + 
  geom_line(linewidth = 1.2, color = "#E5C38A") +
  labs(
    x = "Number of treated observations", 
    y = expression(paste("Average  ", frac("|Estimate|", "|True Effect|"))),
    title = "Evolution of bias with the number of treated observations",
    subtitle = "For statistically significant estimates",
    caption = paste("Fixed sample size:",
                    unique(summary_sim_shocks$N_z)*unique(summary_sim_shocks$N_t),
                    "observations \n")
  )

Magnitude of exaggeration

Let’s then have a quick look at the actual exaggeration and power numbers:

Show code 
summary_sim_shocks |> 
  select(n_treated, power, type_m, median_snr) |> 
  kable(
    col.names = c("Number of treated observations", "Power", "Exaggeration",  "Median SNR"),
    digits = 3
  )
Number of treated observations Power Exaggeration Median SNR
50 6.7 4.523 0.749
100 10.6 3.522 0.844
239 17.6 2.395 1.155
500 34.6 1.704 1.584
1000 57.9 1.328 2.199
2000 85.7 1.089 3.094

Here, the confounding-exaggeration trade-off is driven by the number of treated observations. Let’s explore the exaggeration of our simulation a sample size consistent with that of the literature. In Lavaine and Neidell (2017) there are about 240 treated observations. In my simulations, such a number of treated observations is associated with a rather large exaggeration: about 2.4.

Representativeness of the estimation

I calibrated my simulations to emulate a typical study from this literature. To further check that the results are realistic, I compare the average Signal-to-Noise Ratio (SNR) of the regressions from the simulations to the range of \(t\)-stat of existing studies investigating similar questions. Lavaine and Neidell (2017) find t-stats in the range 0.4 to 2.3 in their table 3 and 4. Currie et al. (2015) find t-stats in the range 0.5 to 4 (both in table 6 but t-stats in this range in table 4 and 5 as well).

As shown in the previous table, I find SNRs in a similar range or even larger and corresponding to substantial exaggeration ratios.

Currie, Janet, Lucas Davis, Michael Greenstone, and Reed Walker. 2015. “Environmental Health Risks and Housing Values: Evidence from 1,600 Toxic Plant Openings and Closings.” American Economic Review 105 (2): 678–709. https://doi.org/10.1257/aer.20121656.
de Chaisemartin, Clément, and Xavier D’Haultfoeuille. 2022. “Two-Way Fixed Effects and Differences-in-Differences with Heterogeneous Treatment Effects: A Survey.” Working {{Paper}} 29691. Working Paper Series. National Bureau of Economic Research. https://doi.org/10.3386/w29691.
Lavaine, Emmanuelle, and Mathew Neidell. 2017. “Energy Production and Health Externalities: Evidence from Oil Refinery Strikes in France.” Journal of the Association of Environmental and Resource Economists 4 (2): 447–77. https://doi.org/10.1086/691554.
Yang, Muzhe, and Shin-Yi Chou. 2018. “The Impact of Environmental Regulation on Fetal Health: Evidence from the Shutdown of a Coal-Fired Power Plant Located Upwind of New Jersey.” Journal of Environmental Economics and Management 90 (July): 269–93. https://doi.org/10.1016/j.jeem.2018.05.005.

References