Abstract
The credibility revolution in economics has made causal inference methods ubiquitous. Simultaneously, an increasing amount of evidence highlights that the literature strongly favors statistically significant results. I show that these two phenomena interact in a way that can substantially worsen the reliability of published estimates: while causal identification strategies alleviate bias caused by confounders, they reduce statistical power and can create another type of bias—exaggeration— when combined with selection on significance. This is consequential as estimates are routinely turned into decision-making parameters for policy makers conducting cost-benefit analyses. I characterize this confounding-exaggeration trade-off theoretically and using realistic Monte Carlo simulations replicating prevailing identification strategies and document its prevalence in the literature. I then discuss potential avenues to address this issue.
Non-technical summary
In this paper, I show that, combined with current academic publication practices, front line empirical methods, while useful and effective to evaluate how a factor causes another, might in some cases lead to conclude that effects are larger than they actually are.
Empirical studies often aim to get a sense of how a factor causes another. For instance, one may want to evaluate the impact of a professional training program on wages. Such effects are often challenging to estimate. A simple difference between the wages of people who participated or not in the program may not reflect the actual wage increase brought by the program; people who took part in the program might have earned higher wages even if they had not received the training. To measure the actual magnitude of the effect of the program, researchers use a particular set of methods. These methods while convincing may be imprecise. They can produce a rather wide range of plausible magnitudes for the effect of the program. If one could reproduce the analysis many times, on average, they would get to the true effect of this training program. Yet, for cost reasons, analyses are often only carried out once. The lack of precision of the methods means that a particular study can produce results that are quite far away from the true effect.
On the other hand, previous research has shown that publication practices favor results that seem ostensibly non null; that is to say far away from zero. Now, if the true effect is close to zero and the study imprecise, the published result will not only be far away from zero but also from the true effect.
The set of methods mentioned above enables to convincingly measure how a factor causes another. However, in this paper, I show that these methods are also more subject to the publication issue described above. In some cases, they may be more likely than conventional methods to produce effect sizes that are too large. I demonstrate that there is a trade-off between measuring an actual causal impact and exaggerating effect sizes as a result of the publication problem discussed above.
To do so, I first illustrate the importance of this trade-off by reviewing several subsets of the economics literature. To study the mechanisms driving this trade-off more precisely, I build simulations, generating fake data representative of real life situations. I have to rely on simulations because to evaluate how far the result of an analysis is from the true effect, one needs to know this true effect. In real life cases, the true effect is never known (otherwise one would not build a study to estimate it). Simulations enable me to define a (fake) ``true effect’’ myself and to vary parameters values to explore the drivers of the trade-off considered. Finally, I derive a formal mathematical proof of the existence trade-off described above and of the impact of its drivers.
To conclude, I discuss potential avenues to avoid exaggerating true effect sizes. Computing and reporting a very simple calculations may help evaluate the risk of exaggeration. I finally develop a tool to highlight the overarching factor that drives the trade-off. This tool enables practitioners to gauge where their study lies with respect to this trade-off.
A Twitter summary
Tweet 1/N
We published a working paper arguing that causal inference methods can produce inflated published estimates.
They intrinsically reduce statistical power. It creates a trade-off between confounding and exaggerating true effect sizes.
Tweet 2/N
When power is low, the distribution of estimates is spread out. Only estimates that are roughly 2 sd away from 0 are statistically significant. Significant estimates overestimate the true effect size.
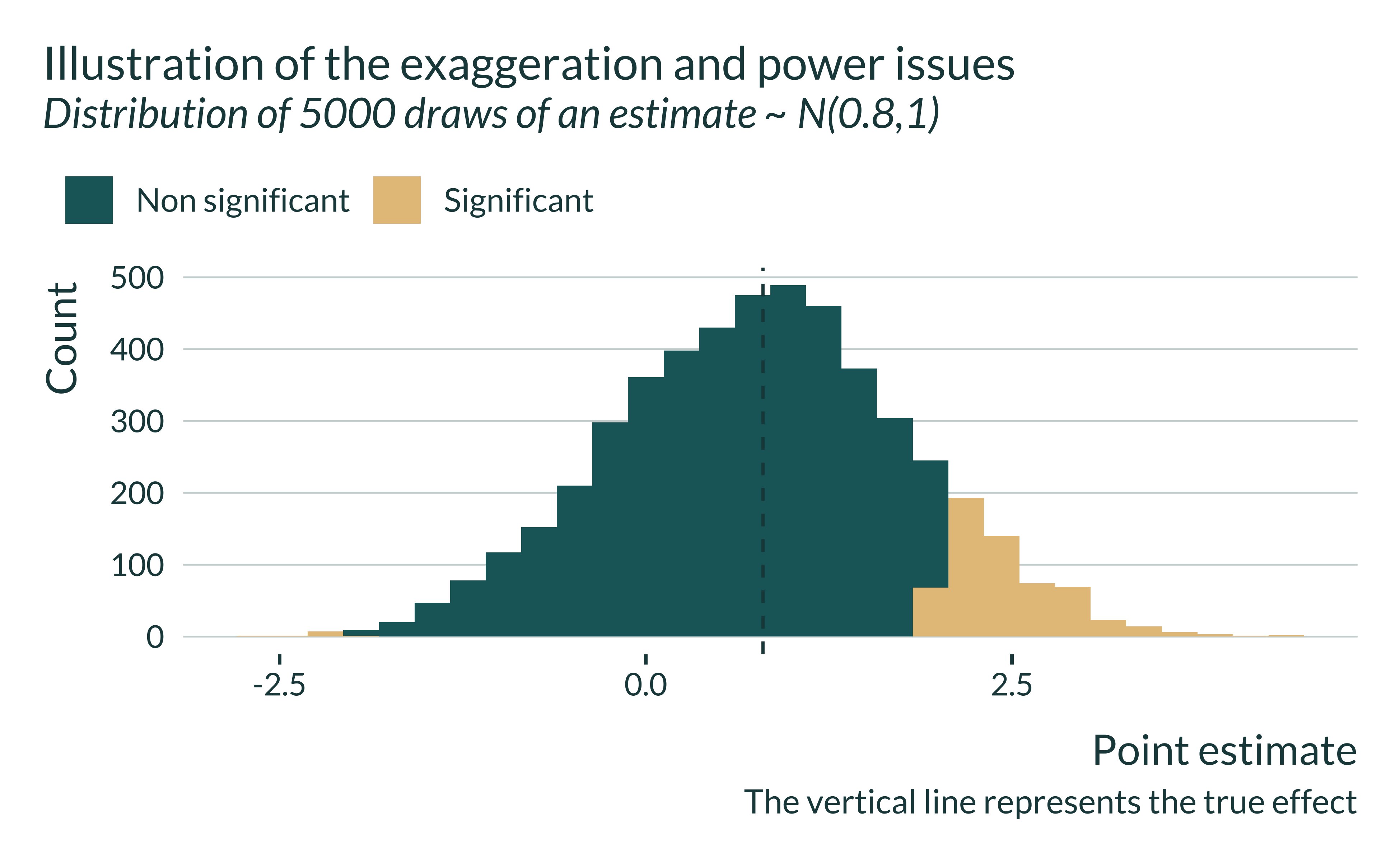
Tweet 3/N
Causal id strat throw out part of the variation, reducing power, leading significant estimates to exaggerate true effects sizes. The same aspect that makes causal identification strategies credible can also induce “bias”.
We build fake data MC simulations to illustrate this.
Tweet 4/N
RDD discards variation by only considering observations within the bandwidth. It decreases the effective sample size.
On average significant estimates may never get close to the true effect.
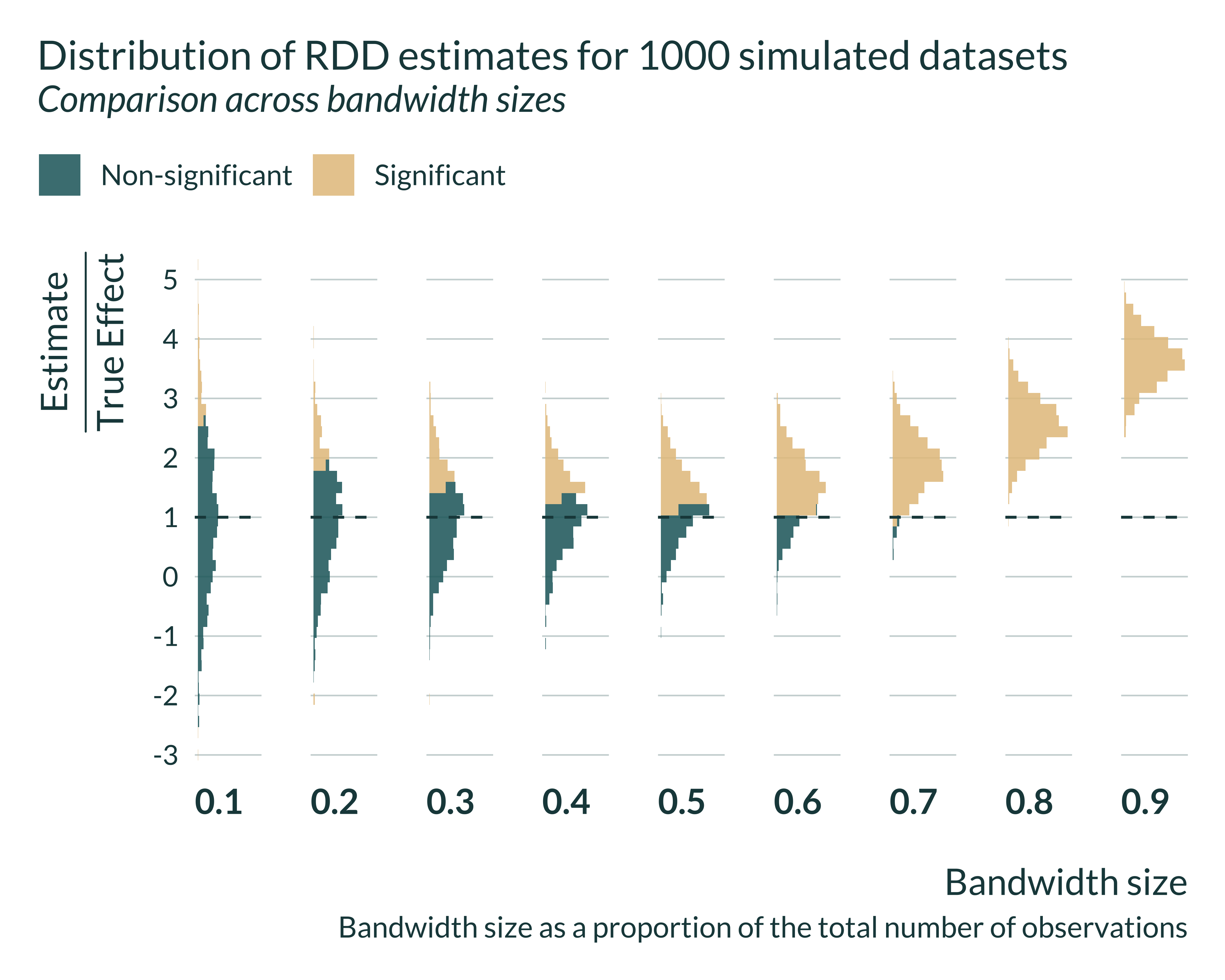
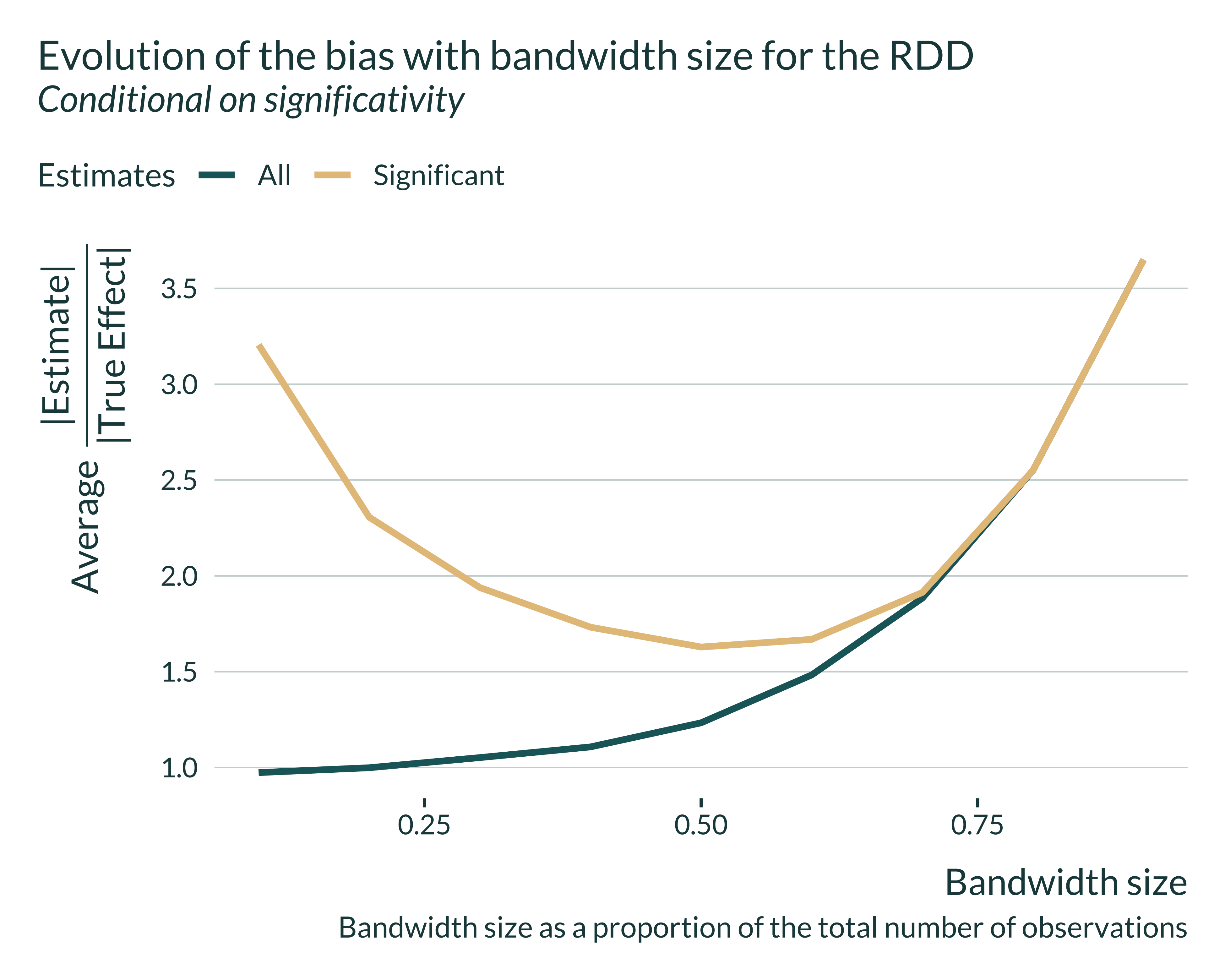
Tweet 5/N
IV only uses part of the variation in the treatment, the portion explained by the instrument. When the “strength” of the instrument is low, the IV is imprecise.
A “naive” OLS can, on average, produce significant estimates that are closer to the true effect than the IV.
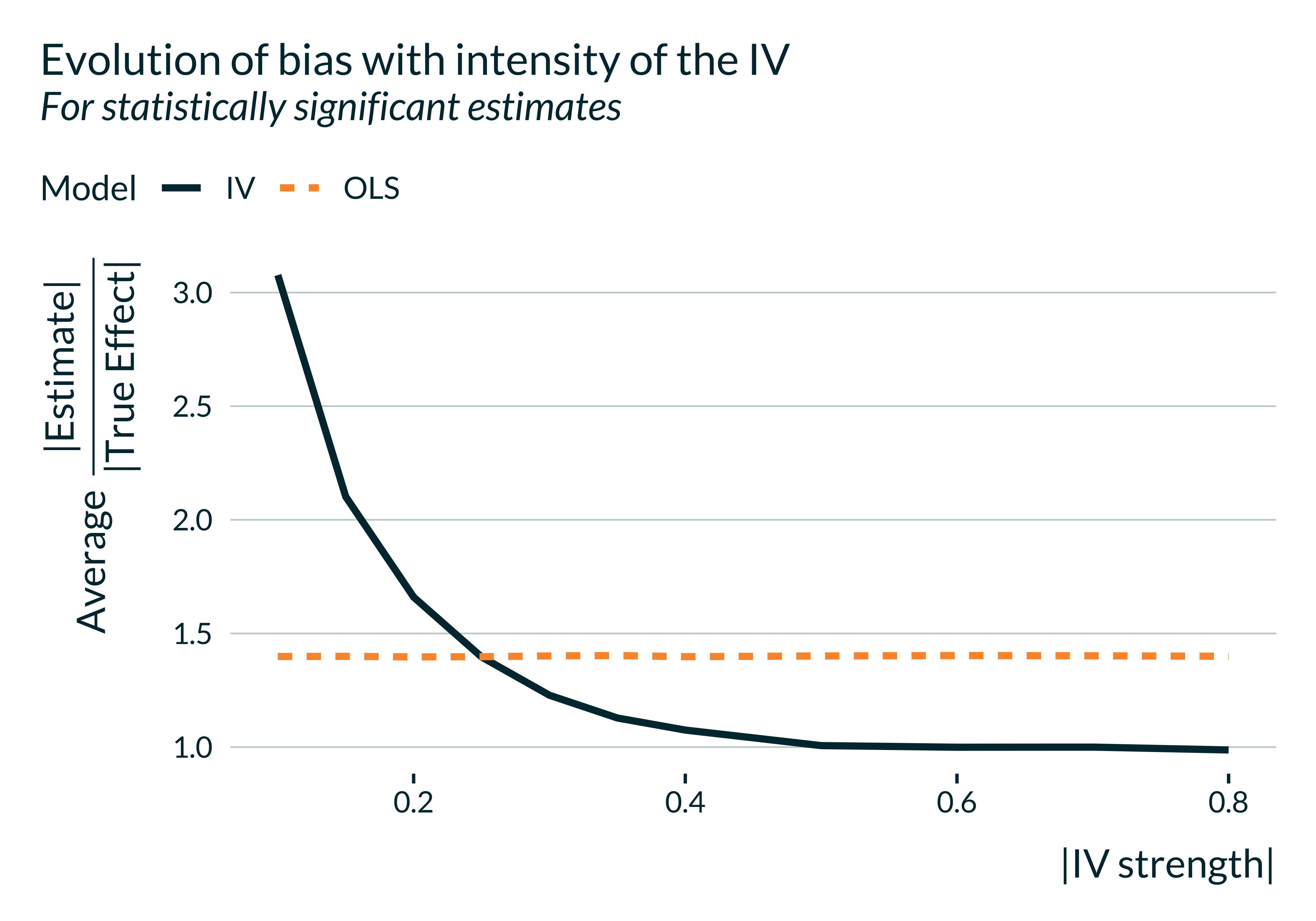
Tweet 6/N
In DiD event studies, the variation used to identify an effect sometimes only comes from a limited number of treated observations. Power can thus be low and estimates inflated.
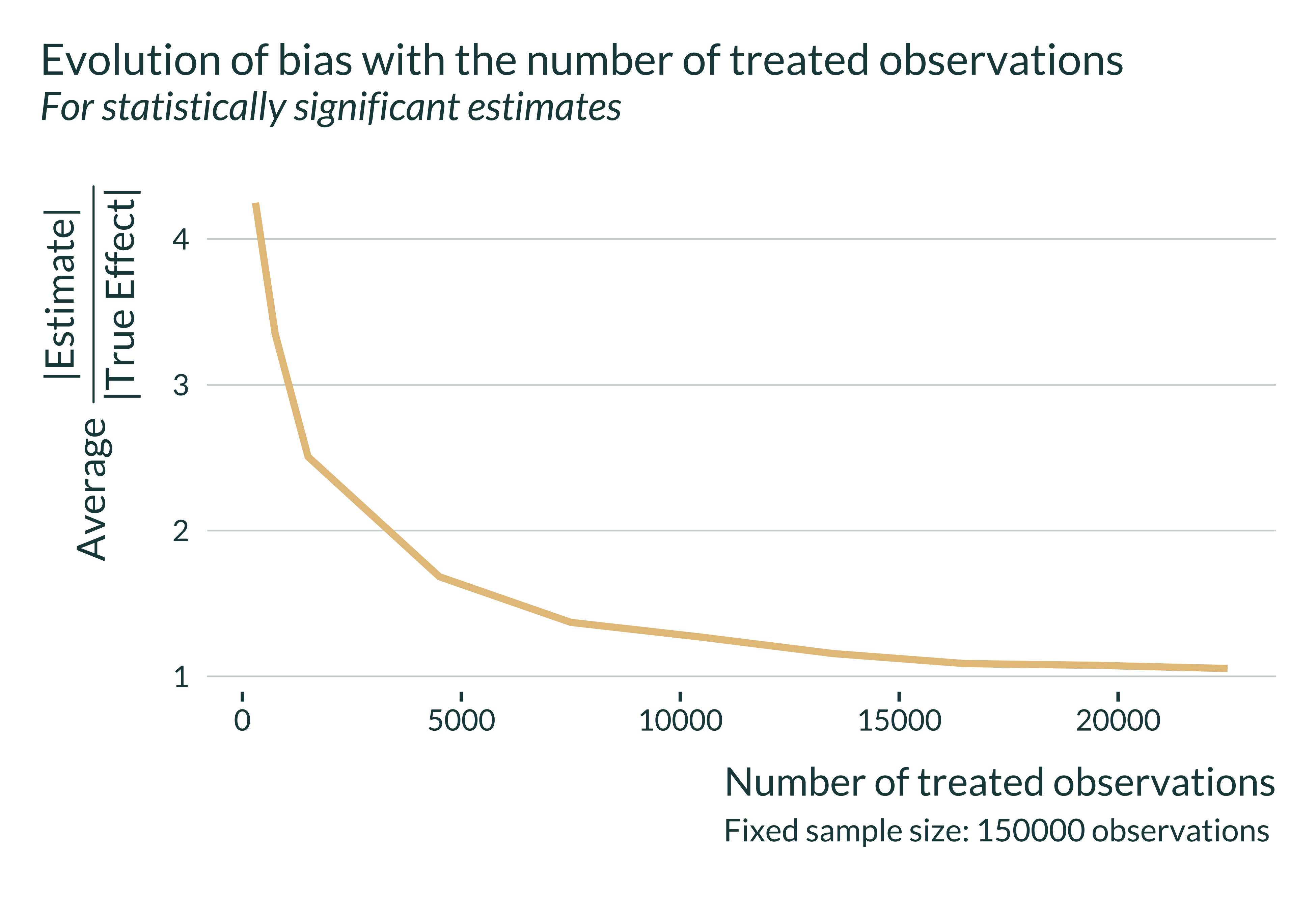
Tweet 7/N
Matching prunes treated units that cannot be matched to untreated ones, reducing the effective sample size.
On average significant estimates may never get close to the true effect.
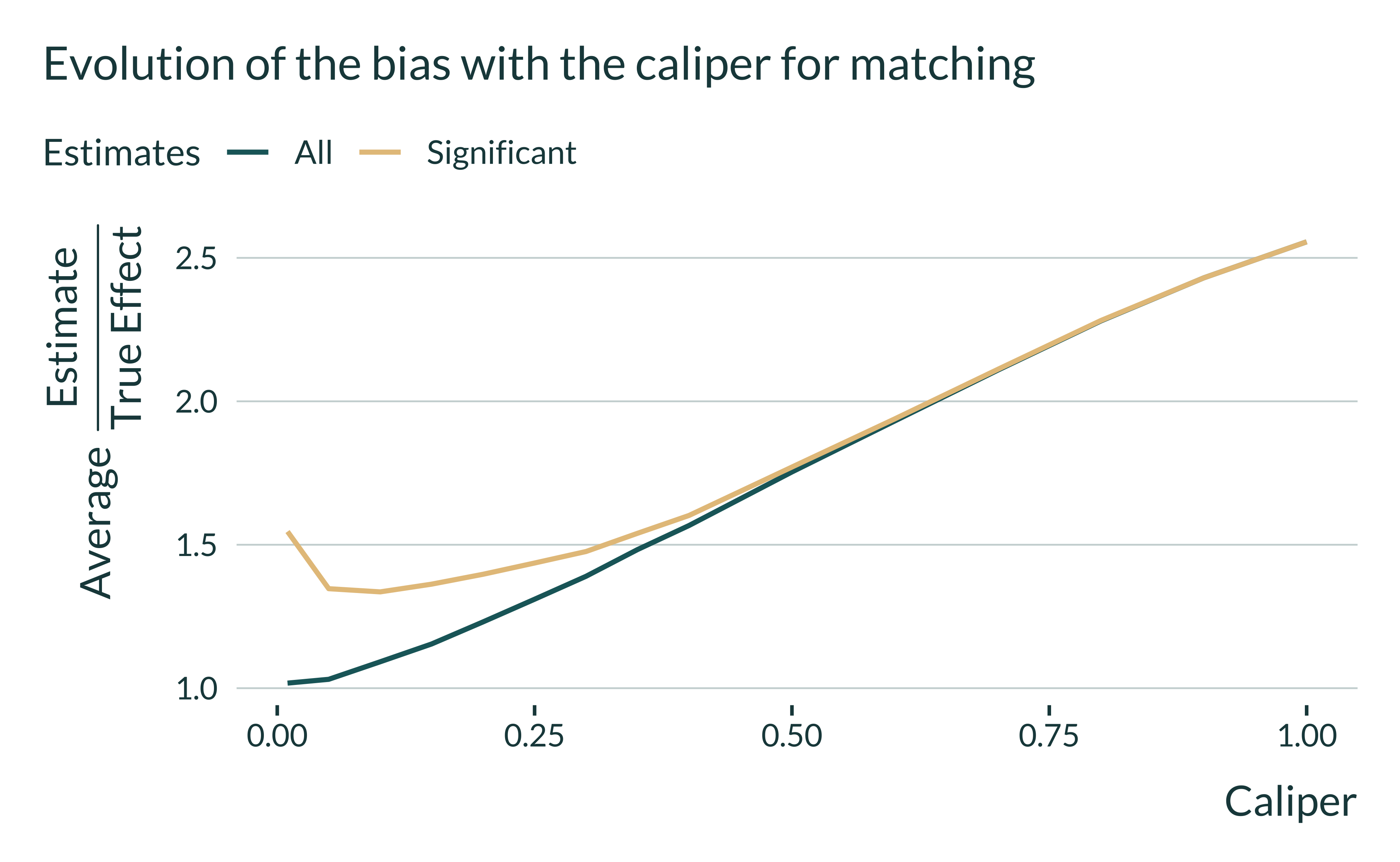
Tweet 8/N
A systematic reporting of pre and post analysis power calculations in observational studies would help gauge the risk of falling into this low power trap.
Tweet N/N
The paper summed up in a picture:
